Definition of Algorithm
The word *Algorithm* means ” A set of finite rules or instructions to be followed in calculations or other problem-solving operations ”
Or
” A procedure for solving a mathematical problem in a finite number of steps that frequently involves recursive operations”.
Therefore Algorithm refers to a sequence of finite steps to solve a particular problem.
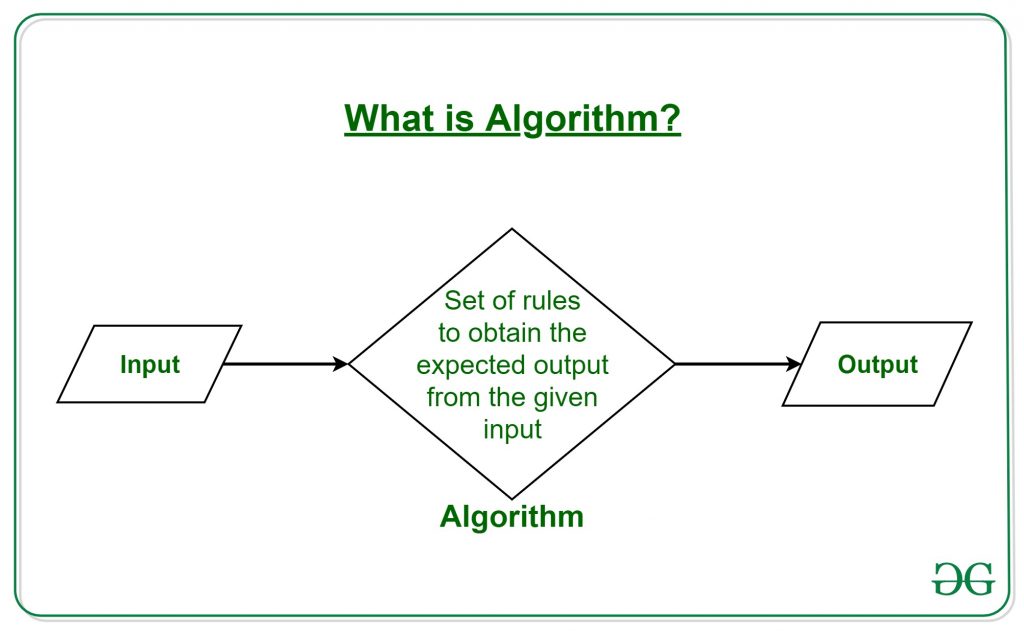
Use of the Algorithms:
Algorithms play a crucial role in various fields and have many applications. Some of the key areas where algorithms are used include:
- *Computer Science:* Algorithms form the basis of computer programming and are used to solve problems ranging from simple sorting and searching to complex tasks such as artificial intelligence and machine learning.
- *Mathematics:* Algorithms are used to solve mathematical problems, such as finding the optimal solution to a system of linear equations or finding the shortest path in a graph.
- *Operations Research*: Algorithms are used to optimize and make decisions in fields such as transportation, logistics, and resource allocation.
- *Artificial Intelligence:* Algorithms are the foundation of artificial intelligence and machine learning, and are used to develop intelligent systems that can perform tasks such as image recognition, natural language processing, and decision-making.
- *Data Science:* Algorithms are used to analyze, process, and extract insights from large amounts of data in fields such as marketing, finance, and healthcare. behavior.
Algorithm Specification-Introduction in Data Structure
An algorithm is defined as a finite set of instructions that, if followed, performs a particular task. All algorithms must satisfy the following criteria
Input. An algorithm has zero or more inputs, taken or collected from a specified set of objects.
Output. An algorithm has one or more outputs having a specific relation to the inputs.
Definiteness. Each step must be clearly defined; Each instruction must be clear and unambiguous.
Finiteness. The algorithm must always finish or terminate after a finite number of steps.
Effectiveness. All operations to be accomplished must be sufficiently basic that they can be done exactly and in finite length.
We can depict an algorithm in many ways.
- Natural language: implement a natural language like English
- Flow charts: Graphic representations denoted flowcharts, only if the algorithm is small and simple.
- Pseudo code: This pseudo code skips most issues of ambiguity; no particularity regarding syntax programming language.
Example 1: Algorithm for calculating factorial value of a number
Step 1: a number n is inputted Step 2: variable final is set as 1 Step 3: final<= final * n Step 4: decrease n Step 5: verify if n is equal to 0 Step 6: if n is equal to zero, goto step 8 (break out of loop) Step 7: else goto step 3 Step 8: the result final is printed
Recursive Algorithms
A recursive algorithm calls itself which generally passes the return value as a parameter to the algorithm again. This parameter indicates the input while the return value indicates the output.
Recursive algorithm is defined as a method of simplification that divides the problem into sub-problems of the same nature. The result of one recursion is treated as the input for the next recursion. The repletion is in the self-similar fashion manner. The algorithm calls itself with smaller input values and obtains the results by simply accomplishing the operations on these smaller values. Generation of factorial, Fibonacci number series are denoted as the examples of recursive algorithms.
Example: Writing factorial function using recursion
intfactorialA(int n) { return n * factorialA(n-1); }
Introduction to Analysis of Algorithms
In theoretical analysis of algorithms, it is common to estimate their complexity in the asymptotic sense, i.e., to estimate the complexity function for arbitrarily large input. The term "analysis of algorithms" was coined by Donald Knuth.
Algorithm analysis is an important part of computational complexity theory, which provides theoretical estimation for the required resources of an algorithm to solve a specific computational problem. Most algorithms are designed to work with inputs of arbitrary length. Analysis of algorithms is the determination of the amount of time and space resources required to execute it.
Usually, the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps, known as time complexity, or volume of memory, known as space complexity.
Analyzing Algorithm Control Structure
To analyze a programming code or algorithm, we must notice that each instruction affects the overall performance of the algorithm and therefore, each instruction must be analyzed separately to analyze overall performance. However, there are some algorithm control structures which are present in each programming code and have a specific asymptotic analysis.
Some Algorithm Control Structures are:
- Sequencing
- If-then-else
- for loop
- While loop
1. Sequencing:
Suppose our algorithm consists of two parts A and B. A takes time tA and B takes time tB for computation. The total computation "tA + tB" is according to the sequence rule. According to maximum rule, this computation time is (max (tA,tB)).
Example:
Suppose tA =O (n) and tB = θ (n2).
Then, the total computation time can be calculated as
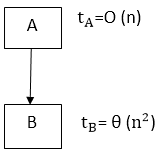 Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
2. If-then-else:
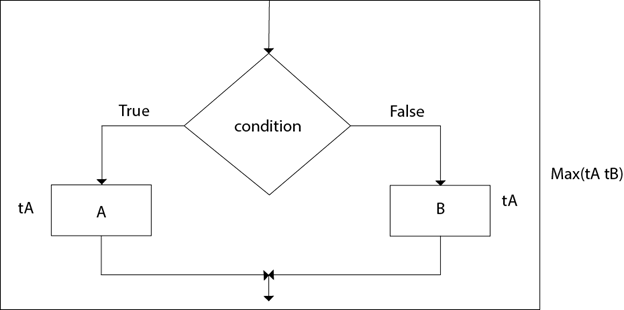
The total time computation is according to the condition rule-"if-then-else." According to the maximum rule, this computation time is max (tA,tB).
Example:
Suppose tA = O (n2) and tB = θ (n2) Calculate the total computation time for the following:
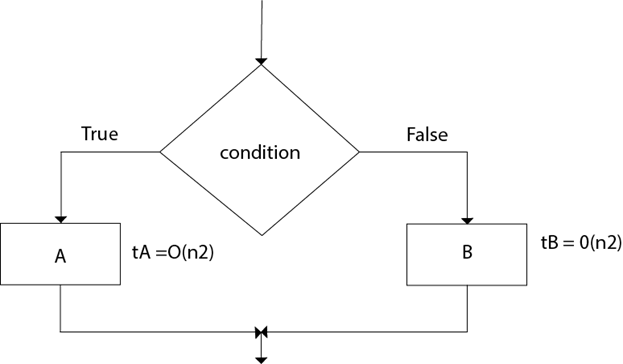
Total Computation = (max (tA,tB)) = max (O (n2), θ (n2) = θ (n2)
3. For loop:
The general format of for loop is:
-
For (initialization; condition; updation)
-
Statement(s);
Complexity of for loop:
The outer loop executes N times. Every time the outer loop executes, the inner loop executes M times. As a result, the statements in the inner loop execute a total of N * M times. Thus, the total complexity for the two loops is O (N2)
Consider the following loop:
- for i ← 1 to n
- {
- P (i)
- }
If the computation time ti for ( PI) various as a function of "i", then the total computation time for the loop is given not by a multiplication but by a sum i.e.
- For i ← 1 to n
- {
- P (i)
- }
Takes 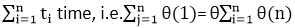
If the algorithms consist of nested "for" loops, then the total computation time is
For i ← 1 to n
{
For j ← 1 to n 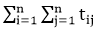 {
P (ij)
}
}
{
P (ij)
}
}
Example:
Consider the following "for" loop, Calculate the total computation time for the following:
- For i ← 2 to n-1
- {
- For j ← 3 to i
- {
- Sum ← Sum+A [i] [j]
- }
- }
Solution:
The total Computation time is:
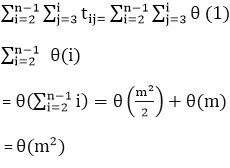
4. While loop:
The Simple technique for analyzing the loop is to determine the function of variable involved whose value decreases each time around. Secondly, for terminating the loop, it is necessary that value must be a positive integer. By keeping track of how many times the value of function decreases, one can obtain the number of repetition of the loop. The other approach for analyzing "while" loop is to treat them as recursive algorithms.
Algorithm:
-
- [Initialize] Set k: =1, LOC: =1 and MAX: = DATA [1]
-
- Repeat steps 3 and 4 while K≤N
-
- if MAX<DATA [k],then:
- Set LOC: = K and MAX: = DATA [k]
-
- Set k: = k+1
- [End of step 2 loop]
-
- Write: LOC, MAX
-
- EXIT
Example:
The running time of algorithm array Max of computing the maximum element in an array of n integer is O (n).
Solution:
- array Max (A, n)
-
- Current max ← A [0]
-
- For i ← 1 to n-1
-
- do if current max < A [i]
-
- then current max ← A [i]
-
- return current max.
The number of primitive operation t (n) executed by this algorithm is at least.
- 2 + 1 + n +4 (n-1) + 1=5n
- 2 + 1 + n + 6 (n-1) + 1=7n-2
The best case T(n) =5n occurs when A [0] is the maximum element. The worst case T(n) = 7n-2 occurs when element are sorted in increasing order.
We may, therefore, apply the big-Oh definition with c=7 and n0=1 and conclude the running time of this is O (n).
Asymptotic Notations and how to calculate them
In mathematics, *asymptotic analysis*, also known as *asymptotics, is a method of describing the limiting behavior of a function. In computing, asymptotic analysis of an algorithm refers to defining the mathematical boundation of its run-time performance based on the input size. For example, the running time of one operation is computed as _f_(n), and maybe for another operation, it is computed as _g_(n*2**). This means the first operation running time will increase linearly with the increase in n and the running time of the second operation will increase exponentially when n increases. Similarly, the running time of both operations will be nearly the same if n** is small in value.
Usually, the analysis of an algorithm is done based on three cases:
- *Best Case (Omega Notation (Ω))*
- *Average Case (Theta Notation (Θ))*
- *Worst Case (O Notation(O))*
All of these notations are discussed below in detail:
*Omega (Ω) Notation:*
Omega (Ω) notation specifies the asymptotic lower bound for a function f(n). For a given function g(n), Ω(g(n)) is denoted by:
Ω (g(n)) = {f(n): there exist positive constants c and n0 such that 0 ≤ c*g(n) ≤ f(n) for all n ≥ n0}.
This means that, f(n) = Ω(g(n)), If there are positive constants n0 and c such that, to the right of n0 the f(n) always lies on or above c*g(n).

Graphical representation
Follow the steps below to calculate Ω for a program:
- Break the program into smaller segments.
- Find the number of operations performed for each segment(in terms of the input size) assuming the given input is such that the program takes the least amount of time.
- Add up all the operations and simplify it, let’s say it is f(n).
- Remove all the constants and choose the term having the least order or any other function which is always less than f(n) when n tends to infinity, let say it is g(n) then, Omega (Ω) of f(n) is Ω(g(n)).
Omega notation doesn’t really help to analyze an algorithm because it is bogus to evaluate an algorithm for the best cases of inputs.
*Theta (Θ) Notation:*
Big-Theta(Θ) notation specifies a bound for a function f(n). For a given function g(n), Θ(g(n)) is denoted by:
Θ (g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0}.
This means that, f(n) = Θ(g(n)), If there are positive constants n0 and c such that, to the right of n0 the f(n) always lies on or above c1g(n) and below c2g(n).

Graphical representation
Follow the steps below to calculate Θ for a program:
- Break the program into smaller segments.
- Find all types of inputs and calculate the number of operations they take to be executed. Make sure that the input cases are equally distributed.
- Find the sum of all the calculated values and divide the sum by the total number of inputs let say the function of n obtained is g(n) after removing all the constants, then in Θ notation, it’s represented as Θ(g(n)).
*Example:* In a linear search problem, let’s assume that all the cases are uniformly distributed (including the case when the key is absent in the array). So, sum all the cases when the key is present at positions 1, 2, 3, ……, n and not present, and divide the sum by n + 1.
Average case time complexity =
⇒
⇒
⇒
Since all the types of inputs are considered while calculating the average time complexity, it is one of the best analysis methods for an algorithm.
*Big – O Notation:*
Big – O (O) notation specifies the asymptotic upper bound for a function f(n). For a given function g(n), O(g(n)) is denoted by:
O (g(n)) = {f(n): there exist positive constants c and n0 such that f(n) ≤ c*g(n) for all n ≥ n0}.
This means that, f(n) = O(g(n)), If there are positive constants n0 and c such that, to the right of n0 the f(n) always lies on or below c*g(n).

Graphical representation
Follow the steps below to calculate O for a program:
- Break the program into smaller segments.
- Find the number of operations performed for each segment (in terms of the input size) assuming the given input is such that the program takes the maximum time i.e the worst-case scenario.
- Add up all the operations and simplify it, let’s say it is *f(n).*
- Remove all the constants and choose the term having the highest order because for *n tends to infinity the constants and the lower order terms in f(n) will be insignificant, let say the function is g(n) then, big-O notation is O(g(n)).*
It is the most widely used notation as it is easier to calculate since there is no need to check for every type of input as it was in the case of theta notation, also since the worst case of input is taken into account it pretty much gives the upper bound of the time the program will take to execute.
Space complexity
Space Complexity
Space complexity is a function describing the amount of memory (space) an algorithm takes in terms of the amount of input to the algorithm.
We often speak of extra memory needed, not counting the memory needed to store the input itself. Again, we use natural (but fixed-length) units to measure this.
We can use bytes, but it's easier to use, say, the number of integers used, the number of fixed-sized structures, etc.
In the end, the function we come up with will be independent of the actual number of bytes needed to represent the unit.
Space complexity is sometimes ignored because the space used is minimal and/or obvious, however sometimes it becomes as important an issue as time complexity.
Definition
Let M be a deterministic Turing machine (TM) that halts on all inputs. The space complexity of M is the function f: N -> N, where f(n) is the maximum number of cells of tape and M scans any input of length M. If the space complexity of M is f(n), we can say that M runs in space f(n).
We estimate the space complexity of a Turing machine by using asymptotic notation.
Let f: N -> R⁺ be a function. The space complexity classes can be defined as follows:
- SPACE = {L | L is a language decided by an O(f(n)) space deterministic TM}
- SPACE = {L | L is a language decided by an O(f(n)) space non-deterministic TM}
- PSPACE is the class of languages that are decidable in polynomial space on a deterministic Turing machine. In other words, PSPACE = ⋃ SPACE (nᵏ)
Savitch's Theorem
One of the earliest theorems related to space complexity is Savitch’s theorem. According to this theorem, a deterministic machine can simulate non-deterministic machines using a small amount of space.
For time complexity, such a simulation seems to require an exponential increase in time. For space complexity, this theorem shows that any non-deterministic Turing machine that uses f(n) space can be converted to a deterministic TM that uses f²(n) space.
Hence, Savitch’s theorem states that, for any function, f: N -> R⁺, where f(n) ≥ n: NSPACE(f(n)) ⊆ SPACE(f(n))
Relationship Among Complexity Classes
The following diagram depicts the relationship among different complexity classes.
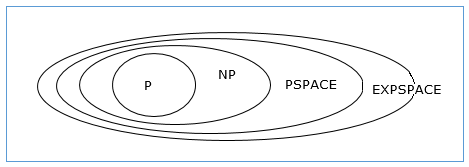
Till now, we have not discussed P and NP classes in this tutorial. These will be discussed later.
Time complexity
Time complexity of an algorithm signifies the total time required by the program to run till its completion.
The time complexity of algorithms is most commonly expressed using the big O notation. It's an asymptotic notation to represent the time complexity. We will study about it in detail in the next tutorial.
Time Complexity is most commonly estimated by counting the number of elementary steps performed by any algorithm to finish execution. Like in the example above, for the first code the loop will run n number of times, so the time complexity will be n atleast and as the value of n will increase the time taken will also increase. While for the second code, time complexity is constant, because it will never be dependent on the value of n, it will always give the result in 1 step.
And since the algorithm's performance may vary with different types of input data, hence for an algorithm we usually use the worst-case Time complexity of an algorithm because that is the maximum time taken for any input size.
Performance measurement
Performance measurement is the process used to assess the efficiency and effectiveness of projects, programs and initiatives. It is a systematic approach to collecting, analyzing and evaluating how “on track” a project/program is to achieve its desired outcomes, goals and objectives.
Performance measurement is typically done by an organization to demonstrate accountability, support decision making and improve processes. Note that It is not an approach that prescribes what must be measured; organizations need to develop their own performance measures based on their project plans and situation.
Performance measurement should be treated as an integral part of any planning process from the outset and should be built into any plan or project that has clear goals and objectives.
Performance measures provide the information to assist in making strategic decisions about what an organization does and how it performs. Performance measurement frameworks are flexible and can be used to measure the effectiveness of a pilot project, a multi-year program or a strategic planning process and can be applied to a new or existing initiative.
Key terminology
Performance measures are also called performance metrics and performance indicators, and the terms can be used interchangeably
Benefits of performance measures
The benefits of measuring performance are numerous and range from measuring the effectiveness of a single project to contributing to a culture of continuous improvement throughout an organization.
Using performance measures on a regular basis helps to inform decisions and means a plan can be adjusted mid-course or priorities can be reset to take advantage of emerging opportunities. An internal performance measurement system will drive results and enable an organization to learn from its successes and failures.
Other benefits of performance measures include:
- Creates “buy-in” through stakeholders setting targets and goals together.
- Develops “best practices” and “lessons learned” that can be applied to future initiatives.
- Increases accountability by demonstrating the effectiveness and value of plans and activities in achieving desired goals/outcomes.
- Informs decision-making including budgeting and resource allocation in an environment where there may be competition over limited resources.
- Helps to demonstrate and document changes over time.
- Helps to communicate an organization’s story.
- Develops relationships through engaging stakeholders and building a common understanding of the process.
Analyzing Control Structure
To analyze a programming code or algorithm, we must notice that each instruction affects the overall performance of the algorithm and therefore, each instruction must be analyzed separately to analyze overall performance. However, there are some algorithm control structures which are present in each programming code and have a specific asymptotic analysis.
Some Algorithm Control Structures are:
- Sequencing
- If-then-else
- for loop
- While loop
1. Sequencing:
Suppose our algorithm consists of two parts A and B. A takes time tA and B takes time tB for computation. The total computation "tA + tB" is according to the sequence rule. According to maximum rule, this computation time is (max (tA,tB)).
Example:
Suppose tA =O (n) and tB = θ (n2).
Then, the total computation time can be calculated as
 Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
Computation Time = tA + tB
= (max (tA,tB)
= (max (O (n), θ (n2)) = θ (n2)
2. If-then-else:

The total time computation is according to the condition rule-"if-then-else." According to the maximum rule, this computation time is max (tA,tB).
Example:
Suppose tA = O (n2) and tB = θ (n2) Calculate the total computation time for the following:

Total Computation = (max (tA,tB)) = max (O (n2), θ (n2) = θ (n2)
3. For loop:
The general format of for loop is:
-
For (initialization; condition; updation)
-
Statement(s);
Complexity of for loop:
The outer loop executes N times. Every time the outer loop executes, the inner loop executes M times. As a result, the statements in the inner loop execute a total of N * M times. Thus, the total complexity for the two loops is O (N2)
Consider the following loop:
- for i ← 1 to n
- {
- P (i)
- }
If the computation time ti for ( PI) various as a function of "i", then the total computation time for the loop is given not by a multiplication but by a sum i.e.
- For i ← 1 to n
- {
- P (i)
- }
Takes 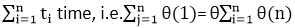
If the algorithms consist of nested "for" loops, then the total computation time is
For i ← 1 to n
{
For j ← 1 to n 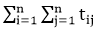 {
P (ij)
}
}
{
P (ij)
}
}
Example:
Consider the following "for" loop, Calculate the total computation time for the following:
- For i ← 2 to n-1
- {
- For j ← 3 to i
- {
- Sum ← Sum+A [i] [j]
- }
- }
Solution:
The total Computation time is:
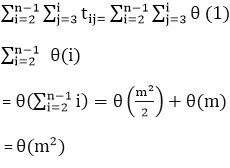
4. While loop:
The Simple technique for analyzing the loop is to determine the function of variable involved whose value decreases each time around. Secondly, for terminating the loop, it is necessary that value must be a positive integer. By keeping track of how many times the value of function decreases, one can obtain the number of repetition of the loop. The other approach for analyzing "while" loop is to treat them as recursive algorithms.
Algorithm:
-
- [Initialize] Set k: =1, LOC: =1 and MAX: = DATA [1]
-
- Repeat steps 3 and 4 while K≤N
-
- if MAX<DATA [k],then:
- Set LOC: = K and MAX: = DATA [k]
-
- Set k: = k+1
- [End of step 2 loop]
-
- Write: LOC, MAX
-
- EXIT
Example:
The running time of algorithm array Max of computing the maximum element in an array of n integer is O (n).
Solution:
- array Max (A, n)
-
- Current max ← A [0]
-
- For i ← 1 to n-1
-
- do if current max < A [i]
-
- then current max ← A [i]
-
- return current max.
The number of primitive operation t (n) executed by this algorithm is at least.
- 2 + 1 + n +4 (n-1) + 1=5n
- 2 + 1 + n + 6 (n-1) + 1=7n-2
The best case T(n) =5n occurs when A [0] is the maximum element. The worst case T(n) = 7n-2 occurs when element are sorted in increasing order.
We may, therefore, apply the big-Oh definition with c=7 and n0=1 and conclude the running time of this is O (n).
Worst, Average and Best Case Analysis of Algorithms
Popular Notations in Complexity Analysis of Algorithms
*1. Big-O Notation*
We define an algorithm’s *worst-case* time complexity by using the Big-O notation, which determines the set of functions grows slower than or at the same rate as the expression. Furthermore, it explains the maximum amount of time an algorithm requires to consider all input values.
*2. Omega Notation*
It defines the *best case* of an algorithm’s time complexity, the Omega notation defines whether the set of functions will grow faster or at the same rate as the expression. Furthermore, it explains the minimum amount of time an algorithm requires to consider all input values.
*3. Theta Notation*
It defines the *average case of an algorithm’s time complexity, the Theta notation defines when the set of functions lies in both O(expression) and Omega(expression)*, then Theta notation is used. This is how we define a time complexity average case for an algorithm.
Measurement of Complexity of an Algorithm
Based on the above three notations of Time Complexity there are three cases to analyze an algorithm:
*1. Worst Case Analysis (Mostly used)*
In the worst-case analysis, we calculate the upper bound on the running time of an algorithm. We must know the case that causes a maximum number of operations to be executed. For Linear Search, the worst case happens when the element to be searched (x) is not present in the array. When x is not present, the search() function compares it with all the elements of arr[] one by one. Therefore, the worst-case time complexity of the linear search would be *O(n)*.
*2. Best Case Analysis (Very Rarely used)*
In the best-case analysis, we calculate the lower bound on the running time of an algorithm. We must know the case that causes a minimum number of operations to be executed. In the linear search problem, the best case occurs when x is present at the first location. The number of operations in the best case is constant (not dependent on n). So time complexity in the best case would be ?(1)
*3. Average Case Analysis (Rarely used)*
In average case analysis, we take all possible inputs and calculate the computing time for all of the inputs. Sum all the calculated values and divide the sum by the total number of inputs. We must know (or predict) the distribution of cases. For the linear search problem, let us assume that all cases are uniformly distributed (including the case of x not being present in the array). So we sum all the cases and divide the sum by (n+1). Following is the value of average-case time complexity.
Iterative Algorithm Analysis
Iterative algorithms are a class of algorithms that repeat a set of instructions or operations until a specific condition is met. These algorithms use iteration, which involves repeating a process multiple times, often with the aim of converging to a solution or achieving a desired result. Iterative algorithms are common in various fields, including computer science, optimization, numerical analysis, and machine learning.
When analyzing iterative algorithms, several key factors are typically considered:
-
Termination Condition: Iterative algorithms continue executing until a certain condition is satisfied. This condition is known as the termination condition. It is crucial to ensure that the algorithm terminates, preventing an infinite loop.
-
Convergence: For many iterative algorithms, especially those used in optimization or numerical methods, convergence is a critical aspect. Convergence refers to the algorithm's ability to approach a specific solution or a desired accuracy as the number of iterations increases.
-
Time Complexity: Time complexity measures the amount of time an algorithm takes to complete as a function of the size of its input. Analyzing the time complexity of an iterative algorithm helps determine its efficiency in terms of execution time.
-
Space Complexity: Space complexity measures the amount of memory an algorithm uses as a function of its input size. It helps assess the algorithm's efficiency in terms of memory usage.
-
Initialization: The initial conditions or starting values can significantly affect the performance and convergence of an iterative algorithm. Proper initialization is often crucial for achieving accurate and efficient results.
-
Optimality: In some cases, iterative algorithms are designed to find optimal solutions. Analyzing whether an algorithm consistently converges to the optimal solution is essential.
-
Stability: Stability is important in iterative algorithms, especially in numerical methods. It ensures that small changes in input or initial conditions do not result in drastic changes in the output.
-
Convergence Rate: The speed at which an iterative algorithm converges to a solution is known as the convergence rate. Faster convergence is generally desirable, especially in real-time or resource-constrained applications.
-
Trade-offs: Consideration of trade-offs between time complexity, space complexity, and accuracy is often necessary. Some algorithms may be more computationally expensive but offer higher accuracy, while others may prioritize speed with some compromise in precision.
-
Parallelization: Assessing the potential for parallelization is crucial, especially in the context of modern computing architectures. Some iterative algorithms can be parallelized to take advantage of multiple processing units, improving overall performance.
Analyzing these aspects helps in understanding the behavior, efficiency, and limitations of iterative algorithms, enabling practitioners to choose the most suitable algorithm for a specific problem.
References
https://www.geeksforgeeks.org/introduction-to-algorithms/ https://www.tutorialspoint.com/algorithm-specification-introduction-in-data-structure https://www.tutorialspoint.com/introduction-to-analysis-of-algorithms https://www.javatpoint.com/daa-analyzing-algorithm-control-structure https://www.geeksforgeeks.org/asymptotic-notations-and-how-to-calculate-them/ https://www.tutorialspoint.com/design_and_analysis_of_algorithms/design_and_analysis_of_algorithms_space_complexities.htm https://www.studytonight.com/data-structures/time-complexity-of-algorithms https://www.ontario.ca/document/performance-measurement-agriculture-agri-food-and-economic-development-organizations/what-performance-measurement https://www.javatpoint.com/daa-analyzing-algorithm-control-structure https://www.geeksforgeeks.org/worst-average-and-best-case-analysis-of-algorithms/